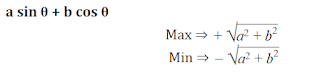Trigonometry Formula in Hindi (त्रिकोणमिति सूत्र हिंदी में):
अंग्रेजी में ऑल ट्रिगोनोमेट्री फॉर्मूला: ट्रिग्नोमेट्री क्वांटिटेटिव एप्टीट्यूड का एक प्रमुख हिस्सा है जो छात्रों को काफी मुश्किल लगता है। त्रिकोणमिति गणित की एक प्रमुख शाखा है जो त्रिभुज के कोणों और लंबाई से संबंधित है। Sin, Cos, Tan, Sec, Cosec, और Cot नाम के कुल 6 त्रिकोणमितीय फलन हैं। इन त्रिकोणमितीय अनुपातों के माध्यम से लंबाई और कोण का पता लगाया जाता है। त्रिकोणमिति के सभी सूत्र, तरकीबें और प्रश्न इन 6 कार्यों से संबंधित हैं। यहां आप त्रिकोणमिति के सूत्र, ट्रिक्स और उस पर आधारित प्रश्न देख सकते हैं।
All Trigonometry Formula in Hindi (सभी त्रिकोणमिति सूत्र हिंदी में)
विभिन्न प्रतियोगी परीक्षाओं जैसे एसएससी, रेलवे आदि में कोण से संबंधित प्रश्न पूछे जाते हैं। इस पोस्ट में, हम आपको परीक्षाओं के लिए उपयोगी त्रिकोणमिति नोट्स प्रदान कर रहे हैं। इससे आपको त्रिकोणमिति के मूल सूत्रों को याद करने में मदद मिलेगी।
Trigonometric Ratios (त्रिकोणमितीय अनुपात):
विभिन्न त्रिकोणमितीय अनुपात फलनों का अध्ययन करने के लिए, हम एक समकोण त्रिभुज लेंगे। माना ABC एक समकोण त्रिभुज है और A = 90°
Values of trigonometric ratios in different quadrants (विभिन्न चतुर्भुजों में त्रिकोणमितीय अनुपातों के मान):
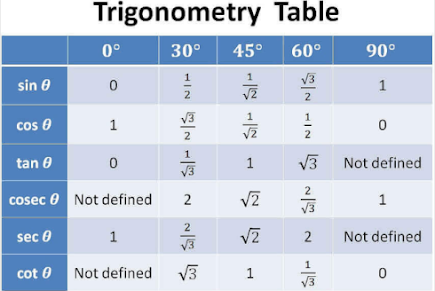
Values of different trigonometric ratios at a certain angle (एक निश्चित कोण पर विभिन्न त्रिकोणमितीय अनुपातों के मान):
0°, 30°, 45°, 60°, 90° कोणों के त्रिकोणमितीय अनुपात के प्रश्न को हल करने के लिए आपको निम्न तालिका याद रखनी होगी।
Relation Between Square Of Different Types Of Trigonometric Ratios (विभिन्न प्रकार के त्रिकोणमितीय अनुपातों के वर्ग के बीच संबंध):
Important Concept to Solve a Specific Type of Question (एक विशिष्ट प्रकार के प्रश्न को हल करने के लिए महत्वपूर्ण अवधारणा):
यदि A + B = 90°
यह हमेशा सच रहेगा:
(i) sin A. sec B = 1 या sin A = cos B
(ii) cos A. cosec B = 1 या sec A = cosec B
(iii) टैन ए। टैन बी = 1 या टैन ए = कोट बी
(iv) खाट ए। खाट बी = 1
(v) sin²A + sin² B = 1
(vi) cos² A + cos² B = 1
Important Formula for Sum and Difference of Two Angles (दो कोणों के योग और अंतर के लिए महत्वपूर्ण सूत्र):
(1) sin (A+B) =sinA. cosB + cosA sinB
(2) sin(A – B) =sinA. cosB – cosA sinB
(3) cos(A+B) =cosA. cosB – sinA sinB
(4) cos(A-B) = cosA. cosB+sinA sinB
(5) 2 sinA.cosB = sin(A+B)+sin (A-B)
(6) 2 cosA. sinB = sin(A+B)-sin (A-B)
(7) 2 sinA. sinB = cos(A-B)-cos(A+B)
(8) 2 cosA.cosB = cos(A+B)+cos(A-B)
(9) sin²A-sin²B = sin(A+B). sin(A-B)
(10) cos²A-cos²B = cos(A+B).cos (A-B)
Different Formula For Tangent
Important Results for Trigonometry (त्रिकोणमिति के लिए महत्वपूर्ण परिणाम):
यदि A + B + C = 180°
तो, tan A + tan B +tan C = tan A. tan B.tan C.
यदि A+ B + C = 90°
तो, cotA + cot B + cot C=cot A. cot B. cot C.
यदि (A) sin + cosec = 2
Minimum | Maximum | |
sin θ, cos θ [odd power] | –1 | +1 |
sin θ, cos θ [even power] | 0 | +1 |
tan θ, cot θ [odd power] | –∞ | +∞ |
tan θ, cot θ [even power] | 0 | +∞ |
sec θ, cosec θ [odd power] | –∞ | +∞ |
sec θ, cosec θ [even power] | +1 | +∞ |
Definition Of Trigonometry (त्रिकोणमिति की परिभाषा)
त्रिकोणमिति गणित की वह शाखा है जो त्रिभुजों से बने त्रिभुजों और बहुभुजों का अध्ययन करती है। त्रिकोणमिति का शाब्दिक अर्थ है 'एक त्रिभुज का मापन' (ग्रीक त्रिकोण से, "त्रिकोण" और मेट्रोन, "माप")। त्रिकोणमिति में सबसे महत्वपूर्ण बात समकोण त्रिभुजों का अध्ययन है। त्रिभुजों और बहुभुजों की भुजाओं की लंबाई और दो भुजाओं के बीच के कोणों के अध्ययन का मुख्य आधार यह है कि किसी समकोण त्रिभुज की किन्हीं दो भुजाओं (आधार, लंब और कर्ण) का अनुपात उस त्रिभुज के कोणों के मान पर निर्भर करता है। त्रिकोणमिति ज्यामिति के प्रसिद्ध बौधायन प्रमेय (पाइथागोरस प्रमेय) से निकटता से संबंधित है।
Trigonometry usage (त्रिकोणमिति उपयोग)
त्रिकोणमिति के कई उपयोग हैं। उदाहरण के लिए, खगोल विज्ञान में, त्रिभुज की तकनीक का उपयोग निकट के तारों से दूरी ज्ञात करने के लिए किया जा सकता है। इसी तरह, भूगोल में त्रिभुज द्वारा स्थलों के बीच की दूरी का पता लगाया जा सकता है। त्रिकोणमिति उपग्रह की सहायता से नेविगेशन में बहुत उपयोगी है। दूसरे शब्दों में, यह कहा जा सकता है कि जिन दूरियों को सीधे मापा नहीं जा सकता है या जिन्हें सीधे मापना बहुत कठिन है, उन दूरियों की गणना त्रिकोणमिति की सहायता से बहुत सटीक रूप से की जा सकती है। इसके लिए कुछ अन्य दूरियाँ और कोण जिन्हें बहुत आसानी से मापा जा सकता है, को मापना पड़ता है।
FAQ On Trigonometry Formula (त्रिकोणमिति सूत्र पर अक्सर पूछे जाने वाले प्रश्न)
Q. त्रिकोणमिति के जनक कौन हैं?
उत्तर: 'गणितज्ञ आर्यभट्ट, त्रिकोणमिति के जनक गोरखपुर में पीछे छूट गए'।
Q. त्रिकोणमिति कैसे की जाती है?
उत्तर: इसके लिए कुछ अन्य दूरियाँ और कोण जिन्हें बहुत आसानी से मापा जा सकता है, को मापना पड़ता है। उदाहरण के लिए, किसी पेड़ की ऊंचाई को सीधे मापना मुश्किल है, फिर जमीन पर एक बिंदु से उस पेड़ की जड़ तक की दूरी और उस बिंदु से पेड़ के शीर्ष तक की दूरी।
Q. त्रिकोणमिति कितने प्रकार की होती है?
उत्तर: त्रिकोणमिति संबंध या अनुपात इस प्रकार है…
sinθ = ओर्थोगोनल = ABAC
cosθ = आधार कर्ण = BCAC
tanθ = लंबवत आधार = ABBC
cotθ = आधार ऊँचाई = BCAB
secθ = कर्ण = ACBC
cosecθ = कोक्लियम = ACAB
Q. त्रिकोणमिति में पाई का मान क्या होता है?
उत्तर : त्रिकोणमिति में पाई का मान 180° होता है।
तो दोस्तों ये थे हमारे All Trigonometry Formula in Hindi (All Formulas of Trigonometry) अगर आपको यह पोस्ट पसंद आई हो तो इसे अपने दोस्तों के साथ शेयर जरूर करें! कृपया कमेंट के माध्यम से बताएं कि आपको यह पोस्ट कैसी लगी, आपके सुझावों का भी स्वागत होगा और हमें कमेंट करके बताएं कि आपका भारत का दौरा कैसा रहा।
Thank you.!! आपको धन्यवाद!